Exercice
Le plan est rapporté à un repère orthonormal ![]()
On désigne par C la courbe représentative de la fonction exponentielle![]() .
.
Pour tout point M d’abscisse t appartenant à C, on considère le point P de coordonnées (t, 0) et le point N, point d’intersection de la tangente en M à C avec l’axe des abscisses.
Montrer que la distance PN est constante.
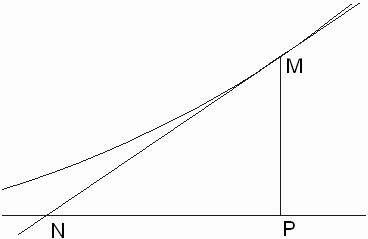
Dans la suite de l’exercice, f désigne une fonction définie sur R, strictement positive, dérivable et dont la dérivée est strictement positive. Pour tout point M d’abscisse t appartenant à la courbe représentative de f, on considère le point P de coordonnées (t, 0) et le point N, point d’intersection de la tangente en M à la courbe représentative de f avec l’axe des abscisses.
(a) Calculer la distance PN en fonction de f (t) et de f '(t).
(b) Déterminer une équation différentielle (Ek) vérifiée par les fonctions f définies sur R, strictement positives, dérivables et dont la dérivée est strictement positive, pour lesquelles la distance PN est une constante k.
(c) Déterminer les fonctions f solutions de (Ek)