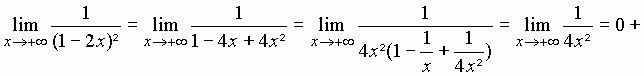
|
Correction Contrôle C#2 |
Exercice I
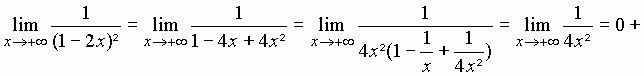
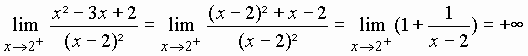
Exercice II
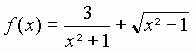
f(x) = sin˛ (x˛)
(sin x˛)' = vou(x) avec u(x) = x˛ et v(X) = sin X donc (sin x˛)' = u'(x)´ v'(u(x)) = 2x ´ cos x˛
Exercice III
1°) a- La fonction f est dérivable sur IR*+ne tant que somme et produit de fonctions dérivables.
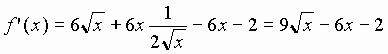
b- On ne peut pas affirmer à priori que la fonction f est dérivable en O car la fonction racine carrée ne l'est pas.
c- La fonction f ' est dérivable sur IR*+ en tant que somme de fonctions dérivables et
Par contre :
et f ' n'est pas dérivable en O.
2°) a- Il n'est pas nécessaire de dériver f '' pour se rendre compte que f '' est décroissante sur IR*+
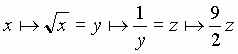
f '' est la composée d'une fonction croissante, d'une fonction décroissante et d'une fonction croissante donc elle est strictement décroissante sur IR*+.
Résolvons l'équation
D'où le tableau de variation :
|
x |
0 |
|
+¥ |
||
|
f ''(x) |
+¥ |
+ |
0 |
– |
–6 |
|
f ' (x) |
–2 |
|
|
 |
–¥ |
On a vu plus haut que f ' est dérivable sur IR*+
Le tableau de variation nous montre que
·
f 'est strictement croissante sur [0 ;] avec f(0)= –2 et
donc f ' est une bijection de [0 ;
] il existe donc un réel a de ]0 ;
·
f ' est strictement décroissante sur [
f ' est une bijection de [
x
–¥
a
b
+¥
f '(x)
–
+
–
f (x)
Figure I : Courbe de la fonction f.
Figure II : Courbe des fonctions f (rouge), f ' (bleu) et f '' (verte)
Exercice IV
car comme
, on a
Didier Aribaud
Colegio Francia
