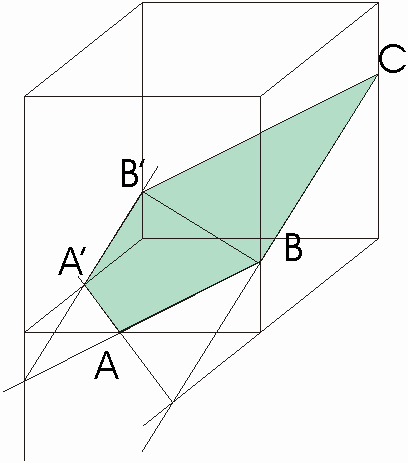
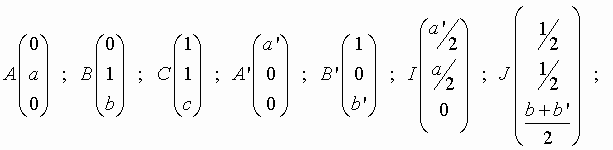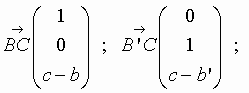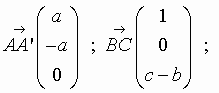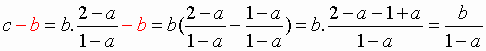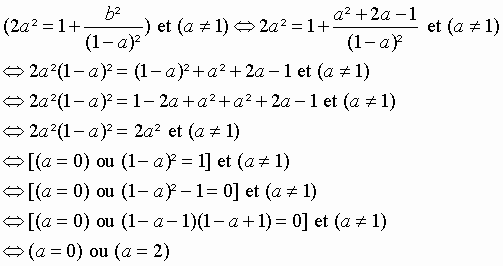1. Sur la figure 1. en annexe ; construire la section du plan (ABC) avec le cube.
2. Le but de l’exercice est d’essayer de répondre à la question : « lorsque la section est un pentagone, celui-ci peut-il être régulier ? »
On considère le cube d’arête 1, et on choisit le repère orthonormé comme sur la figure 2.
Le point A a pour abscisse a ; le point B pour côte b ; et le point C pour côte c.
Le point A’ a pour ordonnée a’ ; le point B’ pour côte b’.
a. Ecrire les coordonnées des points A ; B ; C ; A’ ; B’ ; I et J où I et J sont les milieux respectifs des segments [AA’] et [BB’].
b. Ecrire une condition sur b et b’ pour que BC² = B’C².
(avec 0< b <1 et 0< c <1).
c. Ecrire une condition sur a et a’ pour que de plus, on ait AB² = A’B’².
(avec 0< a <1).
d. Les deux conditions précédentes étant réalisées, écrire une condition sur a et b pour que AA’² = AB². En déduire que b² = a² + 2a – 1

![]()
e. Ecrire une condition pour que I, J et C soient alignés. En déduire que
.
I, J et C alignés ssi les vecteurs
et
(par exemple) colinéaires.
Les vecteurs sont colinéaires donc il existe k réel tel que
on a donc
et
avec a ¹ 1.
f. Ecrire une condition sur a, b et c pour que AA’² = BC². Déduire des questions précédentes, une équation en a que l’on résoudra. Conclure.
(E)
De la relation précédente
on déduit
(E) devient donc :
a ¹ 1
or d’après la question d) on sait que b² = a² + 2a – 1 donc (E) devient :
La seule solution possible est a = 0 car a doit être inférieur à 1.
Le point A serait donc sur le sommet du cube et la section ne serait plus alors un pentagone mais un quadrilatère ce qui est contraire à l’hypothèse de départ. Conclusion : le pentagone ne peut jamais être
régulier.