·
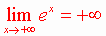
·
Etude de la fonction exponentielle
:1) Sens de variations :
Théorème
: la fonction exp est strictement croissante sur .Démonstration : Valable pour toute bijection strictement croissante.
Soient u et v Î IR ; on a : u = ln ( eu ) et v = ln ( ev ) .
Si u < v alors eu < ev car la fonction ln est strictement croissante ; ( lna < lnb Þ a<b )
Conséquences
: Pour tous réels x et y,ex > ey Û x > y
ex = ey Û x = y
ex > 1 Û x > 0
ex < 1 Û x < 0
2) Etude des limites :
Théorème
:·
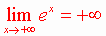
·
Démonstration :
·
Soit M > 0 .Montrons qu’il existe A > 0 tel que si x > A , alors ex > M.
Prenons A = ln M : x > A Þ exp(x) > exp(ln M ) soit exp(x) > M
·
3) Dérivée de exp :
Admettons que exp est dérivable sur .
Alors , ( ln o exp ) (x) = x
En dérivant les deux membres, 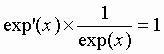
Donc exp’(x) = exp(x) ou encore :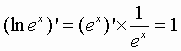
Théorème
: La fonction exp est dérivable sur et égale à sa dérivée.exp’(x) = exp(x)
On dit que exp est une solution de l’équation différentielle y’=y.
5) Comparaison avec la fonction x ® x :
|
Théorème 1 :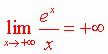 et et 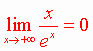
Or
|
Théorème 2 :
|
Didier
Aribaud
Colegio Francia