tirages distincts possibles.Exercice 2.
Un sac contient 10 jetons indiscernables au toucher :
On tire simultanément 4 jetons du sac.
Quel est le nombre de tirages possibles.
On considère que tous les tirages sont équiprobables et on considère les événements suivants :
o
A : "Les 4 numéros sont identiques."o
B : "Avec les jetons tirés on peut former le nombre 2000."o
C : "Tous les jetons sont blancs."o
D : "Tous les jetons sont de la même couleur."o
E : "Au moins un jeton porte un numéro différent des autres."Calculer la probabilité de B
Calculer la probabilité des événements A, C, D et E.
On suppose que l'événement C est réalisé, calculer alors la probabilité de l'événement B.
On établit la règle du jeu suivante :
o
Si le joueur peut former le nombre 7000 il gagne 75€o
Si le joueur peut former le nombre 2000 il gagne 25€o
Si le joueur peut former le nombre 0000 il perd 15€o
Pour tous les autres tirages, il perd 5€G est la variable aléatoire égale au gain du joueur. Etablir la loi de probabilité de G et calculer son espérance mathématique.
Correction
Il y a tirages distincts possibles.
a. 
b. A n'est réalisé que lorsque les 4 jetons portent le numéro 0, il n'y a qu'une possibilité. 
Il y a 6 jetons blancs. La probabilité est donc :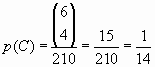 
Les jetons peuvent être, soit tous blancs, soit tous rouges. Or il n'y a que 4 jetons rouges, donc une seule possibilité qu'ils soient tous rouges :
Au moins un jeton porte un numéro différent des autres. Le contraire est "tous les jetons ont le même numéro", qui n'est réalisé que pour le numéro 0.
c. C est réalisé, c'est-à-dire tous les jetons sont blancs. On rappelle que 4 d'entre eux ont le numéro 0 et deux d'entre eux, le numéro 2.
Pour que B soit réalisé, la probabilité est donc de 
, en effet on a 
car on ne peut former 2000 qu'avec des jetons blancs.
3.
Pour 7000 :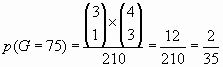
Pour 2000 :
Pour 0000 :
les autres : 
|
G = xi |
–15 |
–5 |
25 |
75 |
|
|
p(G = xi) |
|
|
|
|
1 |
|
pi xi |
|
|
|
|
|
Le joueur peut espérer gagner 0,66 centimes d'Euros par jeu. Celui-ci lui est légèrement favorable.
